求值器完整實作代碼我已經上傳到了GitHub倉庫：TinySCM，感興趣的童鞋可以前往查看，這里順便強烈推薦UC Berkeley的同名課程CS 61A，

即使在變化中，它也絲毫未變，

——赫拉克利特

吾猶昔人，非昔人也，

——僧肇

緒論

在上一篇博客《SICP：元回圈求值器（Python實作）》中，我們介紹了用Python對來實作一個Scheme求值器，然而，我們跳過了部分特殊形式（special forms）和基本程序（primitive procedures）實作的介紹，如特殊形式中的delay、cons-stream，基本程序中的force、streawn-car、stream-map等，事實上，以上特殊形式和基本程序都和惰性求值與流相關，這篇博客我們將介紹如何用Python來實作Scheme中的惰性求值和流，并使用惰性求值的原理來為我們的Scheme解釋器增添尾遞回的支持，

1 Scheme中的流簡介

所謂流，一言以蔽之，就是使用了惰性求值技術的表，它初始化時并沒有完全生成，而是能夠動態地按需構造，從而同時提升程式的計算和存盤效率，

我們先來比較兩個程式，它們都計算出一個區間里的素數之和，其中第一個程式用標準的迭代（尾遞回）風格寫出：

(define (sum-primes a b)
  (define (iter count accum)
    (cond ((> count b) accum)
          ((prime? count) (iter (+ count 1) (+ count accum)))
          (else (iter (+ count 1) accum))))
  (iter a 0))

第二個程式完成同樣的計算，其中使用了我們在博客《SICP: 層次性資料和閉包性質（Python實作）》中所介紹過的序列操作：

(define (sum-primes a b)
  (reduce +
          (filter prime? (enumerate-interval a b))))

在執行計算時，第一個程式只需要維持正在累加的和；而對于第二個程式而言，只有等enumerate-interval構造完這一區間所有整數的表后，filter才能開始作業，而且等過濾區作業完后還得將結果表傳給reduce得到求和，顯然，第一個程式完全不需要像第二個程式這么大的中間存盤，

以上情況還不是最極端的，最極端的情況是下面這種，我們列舉并過濾出了10000到1000000內的所有素數，但實際上只取第二個：

(car (cdr (filter prime?
                    (enumerate-interval 10000 1000000))))

這程式槽點很多，首先要構造與一個大約包含了一百萬個整數的表，然后再通過過濾整個表的方式去檢查每個元素是否是素數，而后只取第二個，幾乎拋棄了全部結果，這在時間和空間上都是極大的浪費，在更傳統的程式設計風格中，我們完全可以交錯進行列舉和過濾，并在找到第二個素數時立即停下來，

流是一種非常巧妙的想法，使我們在保留各種序列操作的同時，不會帶來將序列作為表去操作引起的代價（時間上和空間上的），從表面上看，流也是就是表，但對它們進行操作的程序名字不同，對于流而言有建構式cons-stream，還有兩個選擇函式stream-cdr和stream-cdr，它們對任意的變數x和y都滿足如下的約束條件：

scm> (equal? (stream-car (cons-stream x y)) x)
#t
scm> (equal? (stream-cdr (cons-stream x y)) y)
#t

為了使流的實作能自動透明地完成一個流的構造與使用的交錯進行，我們需要做出一種安排，使得對于流的cdr的求值要等到真正通過程序stream-cdr去訪問它的時候再做，而非在用cons-stream構造流的時候就做，事實上，這一思想在原書2.1.2節中介紹實作有理數的時候也有體現，再那里簡化分子與分母的作業可以在構造的時候完成，也可以在選取的時候完成，這兩種方式將產生同一個資料抽象，但不同的選擇可能產生效率的影響，流和常規表也存在著類似的關系、對于常規的表，其car和cdr都是在構造時求值；而流的cdr則是在讀取時才求值，

我們可以使用流來完成上面所說的素數篩選功能：

scm> (define (stream-enumerate-interval low high)
        (if (> low high)
            nil
            (cons-stream
            low
            (stream-enumerate-interval (+ low 1) high))))
stream-enumerate-interval
scm> (car (cdr (stream-filter prime?
                    (stream-enumerate-interval 10000 1000000))))
10009

2 惰性求值

接下來我們來看如何在求值器中實作流，流的實作將基于一種稱為delay的特殊形式，對于(delay <expr>)的求值將不對運算式<expr>求值，而是回傳一個稱為延時物件（delayed object） 的物件，它可以看做是對在未來（future）求值<expr>的允諾（promise），這種直到需要時才求值的求值策略我們稱之為惰性求值（lazy evaluation） 或 按需呼叫（call-by-need）^[2][3][4]，與之相反的是所謂的急切求值（eager evaluation），也即運算式立即進行求值（除非被包裹在特殊形式中），

注：事實上，future、promise、delay和deferred等來自函式式編程的特性已經被許多語言的并發模塊所吸納^[5]，在并發編程中，我們常常會對程式的執行進行同步，而由于某些計算（或者網路請求）尚未結束，我們需要一個物件（也即future、promise）來代理這個未知的結果，

我們求值器中的延時物件定義為：

class Promise:
    def __init__(self, expr, env):
        self.expr = expr
        self.env = env

    def __str__(self):
        return "#[promise ({0}forced)]".format(
            "not " if self.expr is not None else "")

可以看到，該物件保持了運算式expr及其對應的環境env，但未對其進行求值，

特殊形式delay對應的的求值程序如下，可以看到它回傳了一個Promise延時物件：

def eval_delay(expr, env):
    validate_form(expr, 1, 1)
    return Promise(expr.first, env)

和delay一起使用的還有一個稱為force的基本程序，它以一個延時物件為引數，執行相應的求值作業，也即迫使delay完成它所允諾的求值，

@ primitive("force")
def scheme_force(obj):
    from eval_apply import scheme_eval

    validate_type(obj, lambda x: is_scheme_promise(x), 0, "stream-force")
    return scheme_eval(obj.expr, obj.env)

我們接下來測驗下delay和force：

scm> (define pms1 (delay (+ 2 3)))
pms1
scm> pms1
#[promise (not forced)]
scm> (force pms1)
5
scm> (define pms2 (delay (delay (+ 2 3))))
pms2
scm> (force pms2)
#[promise (not forced)]
scm> (force (force pms2))
5

可見對于(delay (delay (+ 2 3)))這種嵌套的延時物件，也需要像剝洋蔥一樣一層一層地對其進行force，

3 流的實作

3.1 構造流

在實作了最基本的延時物件后，我們用它們來構造流，流由特殊形式cons-stream來構造，該特殊形式對應的求值程序如下：

def eval_cons_stream(expr, env):
    validate_form(expr, 2, 2)
    return scheme_cons(scheme_eval(expr.first, env), Promise(expr.rest.first, env))

可見，在實際使用中(cons-stream <a> <b>)等價于(cons <a> (delay <b>))，也即用序對來構造流，不過序對的cdr并非流的剩余部分的求值結果，而是把需要就可以計算的promise放在那里，

現在，我們就可以繼續定義基本程序stream-car和stream-cdr了：

@primitive("stream-car")
def stream_car(stream):
    validate_type(stream, lambda x: is_stream_pair(x), 0, "stream-car")
    return stream.first

@primitive("stream-cdr")
def stream_cdr(stream):
    validate_type(stream, lambda x: is_stream_pair(x), 0, "stream-cdr")
    return scheme_force(stream.rest)

stream-car選取有關序對的first部分，stream-cdr選取有關序對的cdr部分，并求值這里的延時運算式，以獲得這個流的剩余部分，

3.2 流的行為方式

我們接下來看上述實作的行為方式，我們先來分析一下我們上面提到過的區間列舉函式stream-enumerate-interval的例子，不過它現在是以流的方式重新寫出：

scm> (define (stream-enumerate-interval low high)
        (if (> low high)
            nil
            (cons-stream
            low
            (stream-enumerate-interval (+ low 1) high))))
stream-enumerate-interval

我們來看一下它如何作業，首先，我們使用該程序定義一個流integers，并嘗試直接對其進行求值：

scm> (define integers (stream-enumerate-interval 10000 1000000))
integers
scm> integers
(10000 . #[promise (not forced)])

可見，對于這個流而言，其car是100，而其cdr則是Promise延時物件，其意為如果需要，就能列舉出這個區間里更多的東西，

接下來我們嘗試連續使用stream-cdr遞回地訪問流的cdr部分，以列舉區間里的更多數：

scm> (stream-cdr integers)
(10001 . #[promise (not forced)])
scm> (stream-cdr (stream-cdr integers))
(10002 . #[promise (not forced)])

這個程序實際上就像是剝洋蔥的程序，相當于一層一層地對嵌套的Promise物件進行force，就像下圖^[5]所示的那樣：

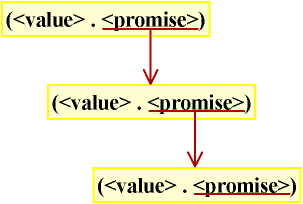
圖中的每個紅色箭頭表示對Promise物件使用一次force，

上面展示的是用流去表示有限長度的序列，但令人吃驚的是，我們甚至可以用流去表示無窮長的序列，比如下面我們定義了一個有關正整數的流，這個流就是無窮長的：

scm> (define (integers-starting-from n)
        (cons-stream n (integers-starting-from (+ n 1))))
integers-starting-from
scm> (define integers (integers-starting-from 1))
integers

在任何時刻，我們都只檢查到它的有窮部分：

scm> integers
(1 . #[promise (not forced)])
scm> (stream-cdr integers)
(2 . #[promise (not forced)])
scm> (stream-cdr (stream-cdr integers))
(3 . #[promise (not forced)])
...

3.3 針對流的序列操作

目前我們已經完成了流的構造，但想實作第一節提到的sum-primes程式我們還需要針對流的map/filter/reduce操作，我們下面即將介紹針對流的stream-map/stream-filter/stream-reduce程序，它們除了操作物件是流之外，其表現和普通的map/filter/reduce完全相同，

stream-map是與程序map類似的針對流的程序，其定義如下：

@primitive("stream-map", use_env=True)
def stream_map(proc, stream, env):
    from eval_apply import complete_apply
    validate_type(proc, is_scheme_procedure, 0, "map")
    validate_type(stream, is_stream_pair, 1, "map")

    def stream_map_iter(proc, stream, env):
        if is_stream_null(stream):
            return nil
        return scheme_cons(complete_apply(proc, scheme_list(stream_car(stream)
                                                            ), env),
                           stream_map_iter(proc, stream_cdr(stream), env))

    return stream_map_iter(proc, stream, env)

stream_map將對流的car應用程序proc，然后需要進一步將程序proc應用于輸入流的cdr，這里對stream_cdr的呼叫將迫使系統對延時的流進行求值，注意，這里我們為了方便延時，使stream_map函式直接回傳用scheme_cons函式構造的普通表，在Scheme的實際實作中回傳的仍然是流，

同理，我們可將stream-filter和stream-reduce函式定義如下：

@primitive("stream-filter", use_env=True)
def stream_filter(predicate, stream, env):
    from eval_apply import complete_apply
    validate_type(predicate, is_scheme_procedure, 0, "filter")
    validate_type(stream, is_stream_pair, 1, "filter")

    def scheme_filter_iter(predicate, stream, env):
        if is_stream_null(stream):
            return nil
        elif complete_apply(predicate, scheme_list(stream_car(stream)), env):
            return scheme_cons(stream_car(stream),
                               scheme_filter_iter(predicate,
                                                  stream_cdr(stream), env))
        else:
            return scheme_filter_iter(predicate, stream_cdr(stream), env)

    return scheme_filter_iter(predicate, stream, env)


@primitive("stream-reduce", use_env=True)
def stream_reduce(op, stream, env):
    from eval_apply import complete_apply
    validate_type(op, is_scheme_procedure, 0, "reduce")
    validate_type(stream, lambda x: x is not nil, 1, "reduce")
    validate_type(stream, is_stream_pair, 1, "reduce")

    def scheme_reduce_iter(op, initial, stream, env):
        if is_stream_null(stream):
            return initial
        return complete_apply(op, scheme_list(stream_car(stream),
                                              scheme_reduce_iter(op,
                                                                 initial,
                                                                 stream_cdr(
                                                                     stream),
                                                                 env)), env)

    return scheme_reduce_iter(op, stream_car(stream), stream_cdr(stream), env)

以下是對stream-map的一個測驗：

scm> (stream-map (lambda (x) (* 2 x))  (stream-enumerate-interval 1 10))
(2 4 6 8 10 12 14 16 18 20)

4 時間的函式式程式觀點

流的使用可以讓我們用一種新的角度去看物件和狀態的問題（參見我的博客《SICP：賦值和區域狀態（Python實作）》），流為模擬具有內部狀態的物件提供了另一種方式，可以用一個流去模擬一個變化的量，例如某個物件的內部狀態，用流表示其順序狀態的時間史，從本質上說，這里的流將時間顯示地表示出來，因此就將被模擬世界里的時間與求值程序中事件發生的順序進行了解耦（decouple），

為了進一步對比這兩種模擬方式，讓我們重新考慮一個“提款處理器”的實作，它管理者一個銀行賬戶的余額，在往期博客中，我們實作了這一處理器的一個簡化版本：

scm> (define (make-simplified-withdraw balance)
       (lambda (amount)
         (set! balance (- balance amount))
         balance))
make-simplified-withdraw
scm> (define W (make-simplified-withdraw 25))
w
scm> (W 20)
5
scm> (W 10)
-5

呼叫make-simplified-withdraw將產生出含有區域狀態變數balance的計算物件，其值將在對這個物件的一系列呼叫中逐步減少，這些物件以amount為引數，回傳一個新的余額值，我們可以設想，銀行賬戶的用戶送一個輸入序列給這種物件，由它得到一系列回傳值，顯示在某個顯示螢屏上，

換一種方式，我們也可以將一個提款處理器模擬為一個程序，它以余額值和一個提款流作為引數，生成賬戶中順序余額的流：

(define (stream-withdraw balance amount-stream)
  (cons-stream
   balance
   (stream-withdraw (- balance (stream-car amount-stream))
                    (stream-cdr amount-stream))))

這里stream-withdraw實作了一個具有良好定義的數學函式，其輸出完全由輸入確定（即不會出現同一個輸入輸出不一致的情況），當然，這里假定了輸入amount-stream是由用戶送來的順序提款值構成的流，作為結果的余額流將被顯示出來，如下展示了根據一個用戶的提款流來完成提款的程序：

scm> (define amount (cons-stream 20 (cons-stream 10 nil)))
amount
scm> (define W (stream-withdraw 25 amount))
w
scm> (stream-cdr W)
(5 . #[promise (not forced)])
scm> (stream-cdr (stream-cdr W))
(-5 . #[promise (not forced)])

可見，從送入這些值并觀看結果的用戶的角度看，這一流程序的行為與由make-simplified-withdraw創建的物件沒有什么不同，當然，在這種流方式里沒有賦值，沒有區域狀態變數，因此也就不會有我們在博客《SICP：賦值和區域狀態（Python實作）》中所遇到的種種理論困難，但是這個系統也有狀態！

這確實是驚人的，雖然stream-withdraw實作了一個定義良好的（well-defined）數學函式，其行為根本不會變化，但用戶看到的卻是在這里與一個改變著狀態的系統互動，事實上，在物理學中也有類似的思想：當我們觀察一個正在移動的粒子時，我們說該粒子的位置（狀態）正在變化，然而，從粒子的世界線^[6]的觀點看，這里根本就不涉及任何變化，

我們知道，雖然用帶有區域狀態變數的物件來對現實世界進行模擬是威力強大且直觀的，但物件模型也產生了對于事件的順序，以及多行程同步的棘手問題，避免這些問題的可能性推動著函式式程式設計語言（functional programming languages） 的開發，這類語言里根本不提供賦值或者可變的（mutable） 資料，在這樣的語言里，所有程序實作的都是它們的引數上的定義良好的數學函式，其行為不會變化，FP對于處理并發系統特別有吸引力，事實上Fortran之父John Backus在1978年獲得圖靈獎的授獎演講^[7]中就曾強烈地推崇FP，而在分布式計算中廣泛應用的Map-Reduce并行編程模型^[8]以及Spark中的彈性分布式資料集（Resilient Distributed Dataset, RDD）^[9]也都受到了FP的影響（關于分布式計算可以參見我的博客《Hadoop：單詞計數(Word Count)的MapReduce實作》和《Spark：單詞計數(Word Count)的MapReduce實作(Java/Python)》），

但是在另一方面，如果我們貼近觀察，就會看到與時間有關的問題也潛入到了函式式模型之中，特別是當我們去模擬一些獨立物件之間互動的時候，舉個例子，我們再次考慮允許公用賬戶的銀行系統的實作，普通系統系統里將使用賦值和狀態，在模擬Peter和Paul共享一個賬戶時，讓他們的交易請求送到同一個銀行賬戶物件，從流的觀點看，這里根本就沒有什么“物件”，我們已經說明了可以用一個計算程序去模擬銀行賬戶，該程序在一個請求交易的流上操作，生成一個系統回應的流，我們也同樣能模擬Peter和Paul有著共同賬戶的事實，只要將Peter的交易請求流域Paul的請求流歸并，并把歸并后的流送給那個銀行賬戶程序即可，如下圖所示：

這種處理方式的麻煩就在于歸并的概念，通過交替地從Peter和Paul的請求中取一個根本不想，假定Paul很少訪問這個賬戶，我們很難強迫Peter去等待Paul，但無論這種歸并如何實作，都必須要在某種Peter和Paul看到的“真實時間”之下交錯歸并這兩個交流，這也就類似原書3.4.1節中引入顯式同步來確保并發處理中的事件是按照“正確”順序發生的，這樣，雖然這里試圖支持函式式的風格來解決問題，但在需要歸并來自不同主體的輸入時，又會將問題重新引入，

總結一下，如果我們要構造出一些計算模型，使其結構能夠符合我們對于被模擬的真實世界的看法，那我們有兩種方法：

• 將這一世界模擬為一集相互分離的、受時間約束的、具有狀態的相互交流的物件，

• 將它模擬為單一的、無時間也無狀態的統一體（unity），

以上兩種方案各有其優勢，但有沒有一種該方法能夠令人完全滿意，我們還等待著一個大一統的出現，

事實上，物件模型對世界的近似在于將其分割為獨立的片段，函式式模型則不沿著物件的邊界去做模塊化，當“物件”之間不共享的狀態遠遠大于它們所共享的狀態時，物件模型就特別好用，這種物件觀點失效的一個地方就是量子力學，再那里將物體看作獨立的粒子就會導致悖論和混亂，將物件觀點與函式式觀點合并可能與程式設計的關系不大，而是與基本認識論有關的論題，

5 用惰性求值實作尾遞回

所謂尾遞回，就是當計算是用一個遞回程序描述時，使其仍然能夠在常量空間中執行迭代型計算的技術，

我們先來考慮下面這個經典的用遞回程序描述的階乘計算：

(define (factorial n)
  (if (= n 1)
      1
      (* n (factorial (- n 1)))))

我們可以利用原書1.1.5節中介紹的代換模型（substitution model），觀看這一程序在計算\(6!\)時所表現出的行為：

可以看出它的代換模型揭示出一種先逐步展開而后收縮的的形狀，如上圖中的箭頭所示，在展開階段里，這一程序構造起一個推遲進行的操作所形成的鏈條（在這里是一個乘法*的鏈條），收縮階段表現為這些運算的實際執行，這種型別的計算程序由一個推遲執行的運算鏈條刻畫，稱為一個遞回計算程序，要執行這種計算程序，解釋器就需要維護好以后將要執行的操作的軌跡，在這個例子中，推遲執行的乘法鏈條的長度也就是為保存其軌跡需要的資訊量，這個長度和計算中所需的步驟數目一樣，都會隨著\(n\)線性增長，這樣的計算程序稱為一個線性遞回程序，

然而，如果遞回呼叫是整個函式體中最后執行的陳述句，且它的回傳值不屬于運算式的一部分，這樣就無需保存將要執行的操作軌跡，從而在常數空間內執行迭代型計算，比如下面這個程序：

(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* counter product)
                 (+ counter 1)
                 max-count)))

我們也用代換模型來查看這一程序在計算\(6!\)時所表現出的行為：

可以看到，該計算程序雖然是用遞回描述的，但并沒有任何增長或者收縮，對于任何一個\(n\)，在計算程序中的每一步，在我們需要保存的軌跡里，所有的東西就是變數product、counter和max-count的當前值，我們稱這種程序為一個迭代計算程序，一般來說，迭代計算程序就是那種其狀態可以用固定數目的狀態變數描述的計算程序；而與此同時，又存在著一套固定的規則，描述了計算程序在從一個狀態到下一個狀態轉換時，這些變數的更新方式；還有一個（可能有的）結束檢測，它描述了這一計算程序應該終止的條件，在計算\(n!\)時，所需的計算步驟隨著\(n\)線性增長，而其使用的空間卻是常量的，這種程序稱為線性迭代程序，

當然，這種當計算用遞回程序描述時，仍能夠在常量空間中執行迭代型計算的特性依賴于底層解釋器的實作，我們將具有這一特性的實作稱為尾遞回的，有了一個尾遞回的實作，我們就可以利用常規的程序呼叫機制表述迭代，這也會使各種復雜的專用迭代結構變成不過是一些語法糖（syntactic sugar） 了，

接下來我們看如何用前文提到的惰性求值技術來為我們的求值器實作尾遞回特性，

乍一看，我們Scheme求值器的scheme_eval()求值函式是用Python語言來遞回定義的：

@primitive("eval", use_env=True)
def scheme_eval(expr, env, _=None):
    # Evaluate self-evaluating expressions
    if is_self_evaluating(expr):
        return expr
    # Evaluate variables
    elif is_scheme_variable(expr):
        return env.lookup_variable_value(expr)

    ...
    # Evaluate special forms
    if is_scheme_symbol(first) and first in SPECIAL_FORMS:
        return SPECIAL_FORMS[first](rest, env)
    # Evaluate an application
    else:
        operator = scheme_eval(first, env)
        # Check if the operator is a macro
        if isinstance(operator, MacroProcedure):
            return scheme_eval(complete_apply(operator, rest, env), env)
        operands = rest.map(lambda x: scheme_eval(x, env))
        return scheme_apply(operator, operands, env)

而我們知道，Python是不支持尾遞回的，但是求值器又必須要依靠Python以這種遞回的方法來撰寫，那怎么在此基礎上為我們的源語言——Scheme語言實作尾遞回呢？答案就在于我們之前提到的Promise延時物件，為了和之前的Promise物件做區分（避免干擾到流的作業），我們將其定義為TailPromise物件，它直接繼承了Promise類，其表現和Promise物件完全相同：

class TailPromise(Promise):
    """An expression and an environment in which it is to be evaluated."""

這里實作尾遞回的訣竅就在于，我們需要使scheme_eval這個程序每次進行遞回呼叫時，都不馬上去進行遞回，而是回傳一個Promise物件，將當前需要求值的運算式expr和環境env暫存起來，之后，我們再在另一個while迭代的回圈里去求值這個Promise物件中含有的運算式，此時的求值需要我們再次呼叫scheme_eval，如果遇到遞回又回傳一個Promise物件，然后回到之前的那個while迭代回圈里再次求值，以此往復，這樣，我們就用延時物件+迭代的回圈在常量空間里去模擬了遞回的求值程序，如下所示：

def optimize_tail_calls(original_scheme_eval):
    def optimized_eval(expr, env, tail=False):
        # If tail is True and the expression is not variable or self-evaluated,
        # return Promise directly, Note that for `optimized_eval`, argument
        # `tail` defaults to False, which means that it is impossible to
        # return Promise at the first call, that is, when the recursion depth
        # is 1
        if tail and not is_scheme_variable(expr) and not is_self_evaluating(
                expr):
            return TailPromise(expr, env)

        # If tail is False or the expression is variable or self-evaluated (
        # which includes the first call of `scheme_eval`), it will be
        # evaluated until the actual value is obtained (instead of Promise)
        result = TailPromise(expr, env)
        while (isinstance(result, TailPromise)):
            # A call to `original_scheme_eval` actually can simulate the
            # recursion depth plus one.
            result = original_scheme_eval(result.expr, result.env)
        return result

    return optimized_eval


# Uncomment the following line to apply tail call optimization
scheme_eval = optimize_tail_calls(scheme_eval)

這里為了不直接修改scheme_eval的內容，使用一個Python閉包的技巧，也就是使optimized_eval成為原始scheme_eval的函式裝飾器，從而在其基礎上添加尾遞回功能并對其進行替代，上述代碼實際上就等同于：

from functools import wraps
def optimize_tail_calls(original_scheme_eval):
    @wraps(original_scheme_eval)
    def optimized_eval(expr, env, tail=False):
        ...
        return result

    return optimized_eval

@optimize_tail_calls
@primitive("eval", use_env=True)
def scheme_eval(expr, env, _=None):
    ...

接下來我們測驗一下我們求值器的尾遞回功能：

scm> (define (sum n total)
            (if (zero? n) total
              (sum (- n 1) (+ n total))))
sum
scm> (sum 1000001 0)
500001500001

可以看到尾遞回特性已經成功地實作了，

OK，我們已經實作好了尾遞回功能，這依賴于底層惰性求值的實作，但是別忘了，我們有時候是不需要惰性求值，而是需要急切求值的（也即求值結果不能是TailPromise物件），比如在對MacroProcedure程序物件（該程序物件由宏的定義產生）進行實際應用前，我們需要先將宏的內容進行進行展開，而這就需要我們另外定義一個complete_apply函式：

def complete_apply(procedure, args, env):
    val = scheme_apply(procedure, args, env)
    if isinstance(val, TailPromise):
        return scheme_eval(val.expr, val.env)
    else:
        return val

該函式可在給定環境env下將程序procedure應用到實參arguments，知道結果不是TailPromise物件為止，然后就得到了我們在scheme_eval()函式中對宏的處理方式：

if isinstance(operator, MacroProcedure):
    return scheme_eval(complete_apply(operator, rest, env), env)

注意，scheme-map/scheme-filter/scheme-reduce和stream-map/stream-filter/stream-reduce這幾個基本程序函式要傳入一個程序物件為引數，而在這幾個函式中對該程序物件的應用就必須得是急切的，這是因為optimize_tail_calls函式中的while迭代回圈只能保證map/filter/reduce等基本程序運算式本身得到求值，而對這些基本程序所呼叫的高階程序的實際應用是得不到保障的，以map基本程序為例，如果仍使用惰性求值的scheme_apply來完成程序物件的應用：

@ primitive("map", use_env=True)
def scheme_map(proc, items, env):
    ...
    def scheme_map_iter(proc, items, env):
        if is_scheme_null(items):
            return nil
        return scheme_cons(scheme_apply(proc, scheme_list(items.first), env),
                           scheme_map_iter(proc, items.rest, env))

    return scheme_map_iter(proc, items, env)

那么我們將得到如下結果：

scm> (map (lambda (x) (* 2 x))  (list 1 2 3))
(#[promise (not forced)] #[promise (not forced)] #[promise (not forced)])

可以看到map這個基本程序運算式是得到求值了，但其所呼叫的高階程序(lambda (x) (* 2 x))并未得到實際應用，

解決之道很簡單，在scheme-map/scheme-filter/scheme-reduce幾個函式中，對程序物件進行求值時使用complete-apply即可，比如對scheme-map而言，就需要使用complete-apply做如下修改：

@ primitive("map", use_env=True)
def scheme_map(proc, items, env):
    ...
    def scheme_map_iter(proc, items, env):
        if is_scheme_null(items):
            return nil
        return scheme_cons(complete_apply(proc, scheme_list(items.first), env),
                           scheme_map_iter(proc, items.rest, env))

    return scheme_map_iter(proc, items, env)

這樣，再對map基本程序進行測驗，就能夠得到正確的求值結果了：

scm> (map (lambda (x) (* 2 x))  (list 1 2 3))
(2 4 6)

參考

• [1] Abelson H, Sussman G J. Structure and interpretation of computer programs[M]. The MIT Press, 1996.
• [2] 8.6 Lazy evaluation
• [3] Wiki: Lazy evaluation
• [4] Yet Another Scheme Tutorial: 17. Lazy evaluation
• [5] Wiki: Futures and promises
• [6] Wiki: World line
• [7] Backus J. Can programming be liberated from the von Neumann style? A functional style and its algebra of programs[J]. Communications of the ACM, 1978, 21(8): 613-641.
• [8] Dean J, Ghemawat S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113.
• [9] Zaharia M, Chowdhury M, Das T, et al. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing[C]//Presented as part of the 9th {USENIX} Symposium on Networked Systems Design and Implementation ({NSDI} 12). 2012: 15-28.

標籤：其他

上一篇：使用 Async Rust 構建簡單的 P2P 節點

下一篇：返回列表