Curve _fitting
前幾天在作業的時候接到了一個需求,希望將不同坐標系,不同角度的兩條不規則曲線,并且組成該曲線的點集數量不一致,需求是希望那個可以通過演算法的平移和旋轉搞到一個概念里最貼合,擬合態進行比較,
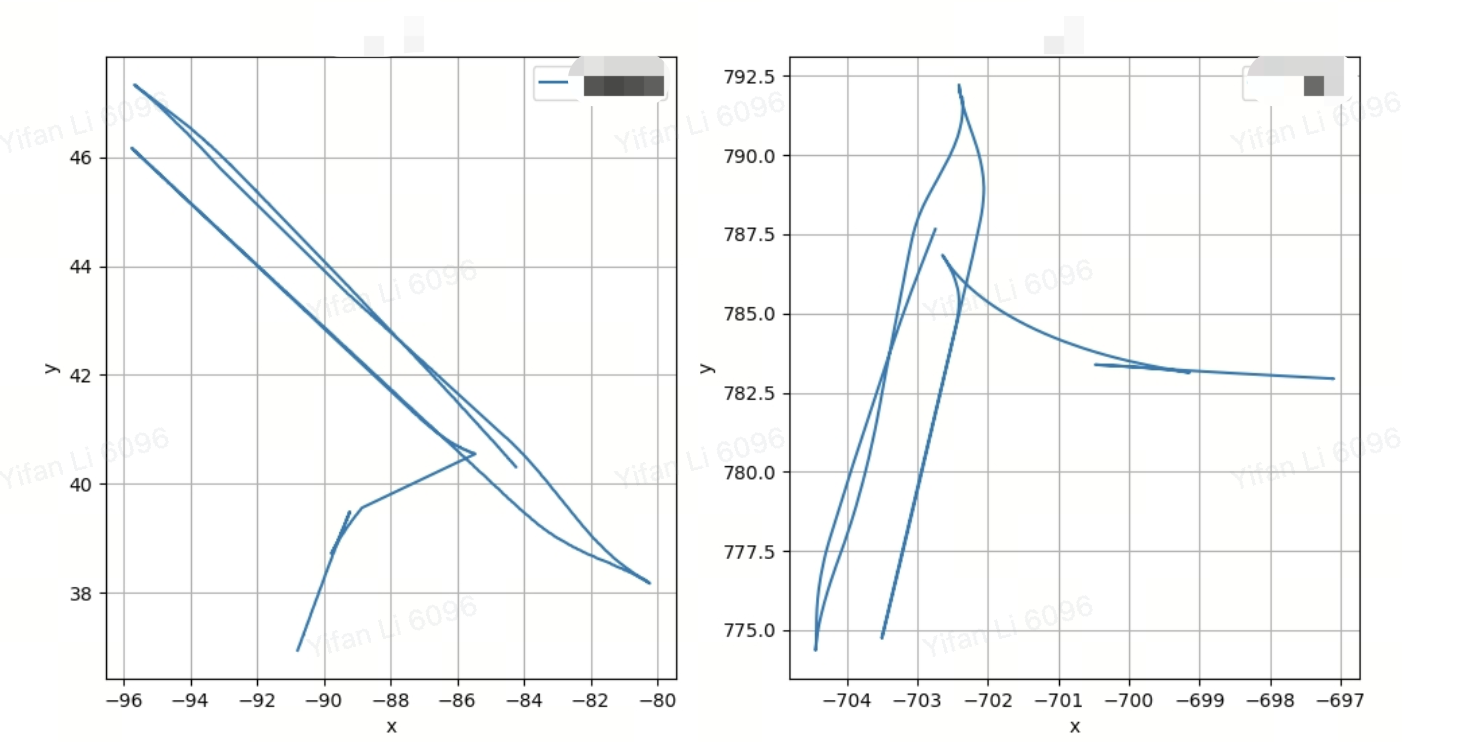
這是初步將兩組資料畫到圖里的情況,和背景需求是一致的,其實從肉眼看過去左圖逆時針旋轉120度可以得到一個大致差不多的圖,
但這里存在了兩個問題:
- 就算搞到了同一個坐標系,一個基準點選取在哪里,影像繞著這個點旋轉才可以得到最擬合點樣子
- 找到基準點,判斷最擬合的標準是什么,怎么算距離
首先我們將兩圖換到一個相同坐標系下
def Convert_to_the_same_scale(xs1, ys1, xs2, ys2):
xs1 = np.array(xs1)
ys1 = np.array(ys1)
xs2 = np.array(xs2)
ys2 = np.array(ys2)
# 減去平均值,使得資料中心化
xs1 -= np.mean(xs1) # 算一個平均值,最后回到0,0坐標系下
ys1 -= np.mean(ys1)
xs2 -= np.mean(xs2)
ys2 -= np.mean(ys2)
# 除以標準差,使得資料標準化
xs1 /= np.std(xs1)
ys1 /= np.std(ys1)
xs2 /= np.std(xs2)
ys2 /= np.std(ys2)
return xs1.tolist(), ys1.tolist(), xs2.tolist(), ys2.tolist()
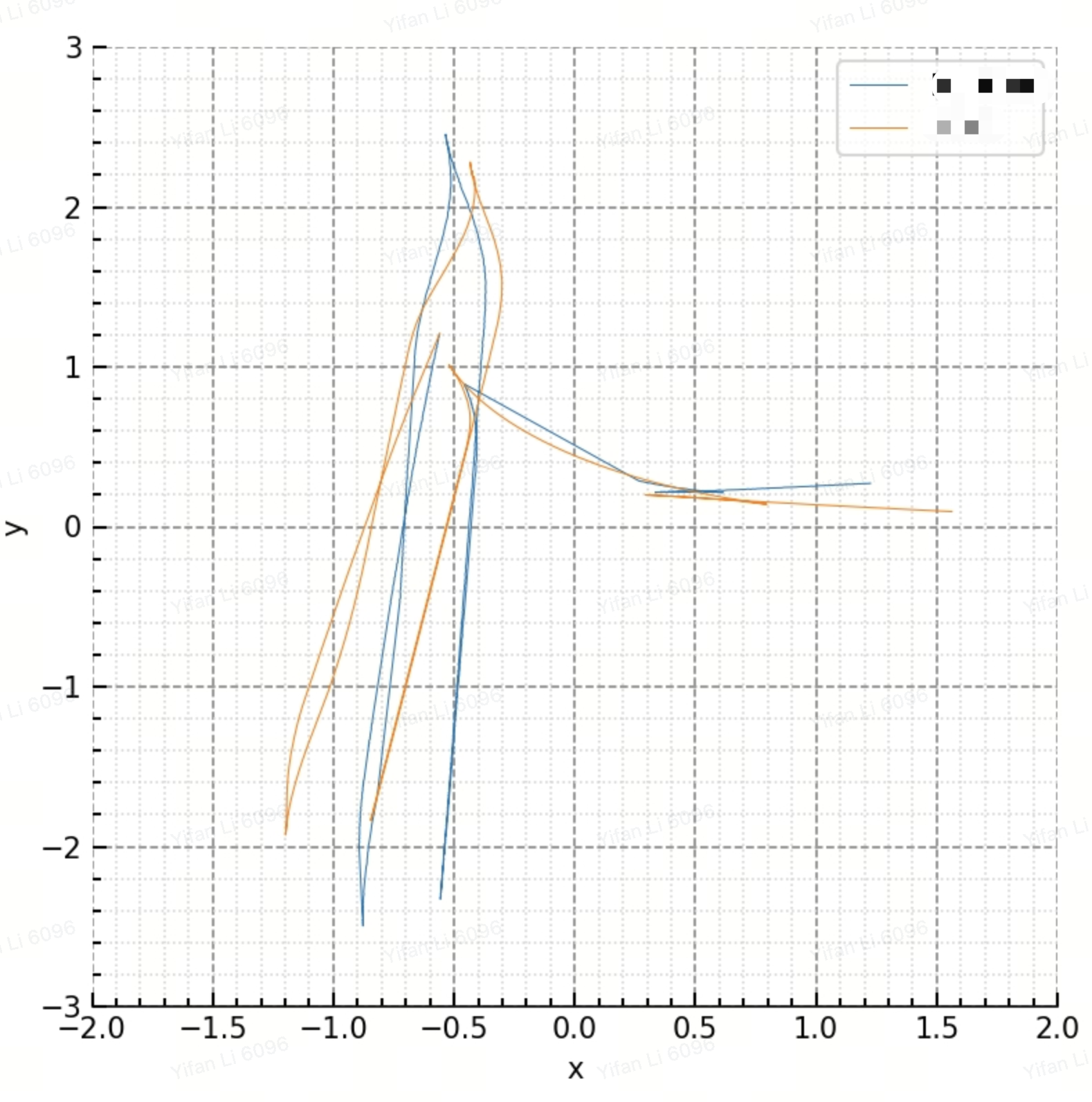
我們運用numpy中的函式進行了資料中心化和標準化的處理,np.std()函式是Numpy庫中的一個方法,它被用來計算陣列中元素的標準差,標準差是一種衡量資料分散程度的指標,值越大表明資料越分散,將資料點除以該數值可以統一到一個離散的程度,經過處理之后得到了以下圖樣:

接下來就要引入一個比較熱的判斷距離的演算法DTW,DTW是指動態時間扭曲(Dynamic Time Warping)演算法,這是一種用于測量兩個可能不等長的序列之間相似度的演算法,該演算法可以找到序列之間的對齊方式,使得對齊后的總體誤差最小,
在信號處理、識別和資料挖掘領域,DTW廣泛應用于各種任務,如語音識別和手寫數字識別,它的主要優點是能夠處理時間序列的“彈性”對齊問題,即即使在時間尺度上存在變形,也能夠匹配和識別模式,
DTW 演算法的基本步驟如下:
- 初始化:創建一個二維矩陣,其中行數和列數分別等于兩個輸入序列的長度,將第一個元素設為 0,其余元素設為無窮大,
- 遞回填充:從左上角開始,計算當前位置的距離(通常是歐氏距離),并將其與左方、上方、左上方三個元素的最小值相加,結果存盤在當前位置,
- 尋找路徑:從右下角開始,向左上角回溯,尋找最小累計距離的路徑,這就是兩個序列之間的最佳對齊路徑,
- 輸出距離:回傳最后一個元素的值,即為兩個序列之間的 DTW 距離,
值得注意的是,盡管 DTW 可以很好地處理變化的速度和非線性變形,但是它對輸入序列的噪聲和例外值敏感,并且計算成本相當高,
我這兩個影像都是由幾千個點組成的,所以如果讓DTW演算法去自己360度無死角找best angle和最擬合的點的話,計算量就太大了,
所以經過一些計算,我可以先拿到兩組點的端點,將起點對齊之后,再去將一條線以另一條線為準進行旋轉,此時得到的角度可以被視作是一個范圍角度,
def get_degree(a,b,c,d):
def get_vector_from_points(p1, p2):
return np.array([p2[0] - p1[0], p2[1] - p1[1]])
def dot_product(v1, v2):
return np.dot(v1, v2)
def cross_product(v1, v2):
return v1[0]*v2[1] - v1[1]*v2[0]
def length_of_vector(v):
return np.linalg.norm(v)
def translate_point(p, t):
return [p[0]+t[0], p[1]+t[1]]
def rotate_point(p, angle):
px, py = p
cos_theta = np.cos(angle)
sin_theta = np.sin(angle)
qx = cos_theta * px - sin_theta * py
qy = sin_theta * px + cos_theta * py
return [qx, qy]
def align_lines(A, B, C, D):
# Step 1: Translate
T = get_vector_from_points(C, A)
C_translated = translate_point(C, T)
D_translated = translate_point(D, T)
# Step 2: Rotate
vAB = get_vector_from_points(A, B)
vCD = get_vector_from_points(C_translated, D_translated)
cos_theta = dot_product(vAB, vCD) / (length_of_vector(vAB)*length_of_vector(vCD))
theta = np.arccos(cos_theta)
direction = np.sign(cross_product(vAB, vCD))
C_final = rotate_point(C_translated, direction*theta)
D_final = rotate_point(D_translated, direction*theta)
return np.degrees(direction*theta)
degree = align_lines(a,b,c,d)
return degree
rotate_bosch = [[BOSCH_xs[0],BOSCH_ys[0]],[BOSCH_xs[-1],BOSCH_ys[-1]]]
rotate_ego = [[EGO_xs[0],EGO_ys[0]],[EGO_xs[-1],EGO_ys[-1]]]
theta = (get_degree(rotate_ego[0],rotate_ego[1],rotate_bosch[0],rotate_bosch[1]))
tran_x = EGO_xs[0] - BOSCH_xs[0]
tran_y = EGO_ys[0] - BOSCH_ys[0]
這段代碼定義了一個名為 get_degree 的函式,其目的是計算兩條線之間的夾角,這里的引數 a,b,c,d 分別代表兩條線上的四個點,其中 a 和 b 在一條線上,c 和 d 在另一條線上,
下面是該函式的詳細步驟:
- 定義輔助函式:這些函式用于執行向量運算、平移和旋轉點等操作,
- 定義主要流程:在
align_lines函式中,首先通過向量差得到平移量T,將c和d兩點進行平移,使得平移后的c點與a點重合;接著計算AB和CD兩向量的夾角theta,并確定旋轉方向direction;最后根據direction*theta對平移后的c和d進行旋轉,該函式回傳的是theta的度數形式, - 呼叫主要流程:在
get_degree函式中,呼叫align_lines函式并回傳得到的角度,
簡單來說,這段代碼就是把以 c 和 d 為端點的線段通過平移和旋轉,讓它和以 a 和 b 為端點的線段對齊,然后回傳這個旋轉的角度,獲取的角度就是一個比較貼合的角度,但是不是最精準的,
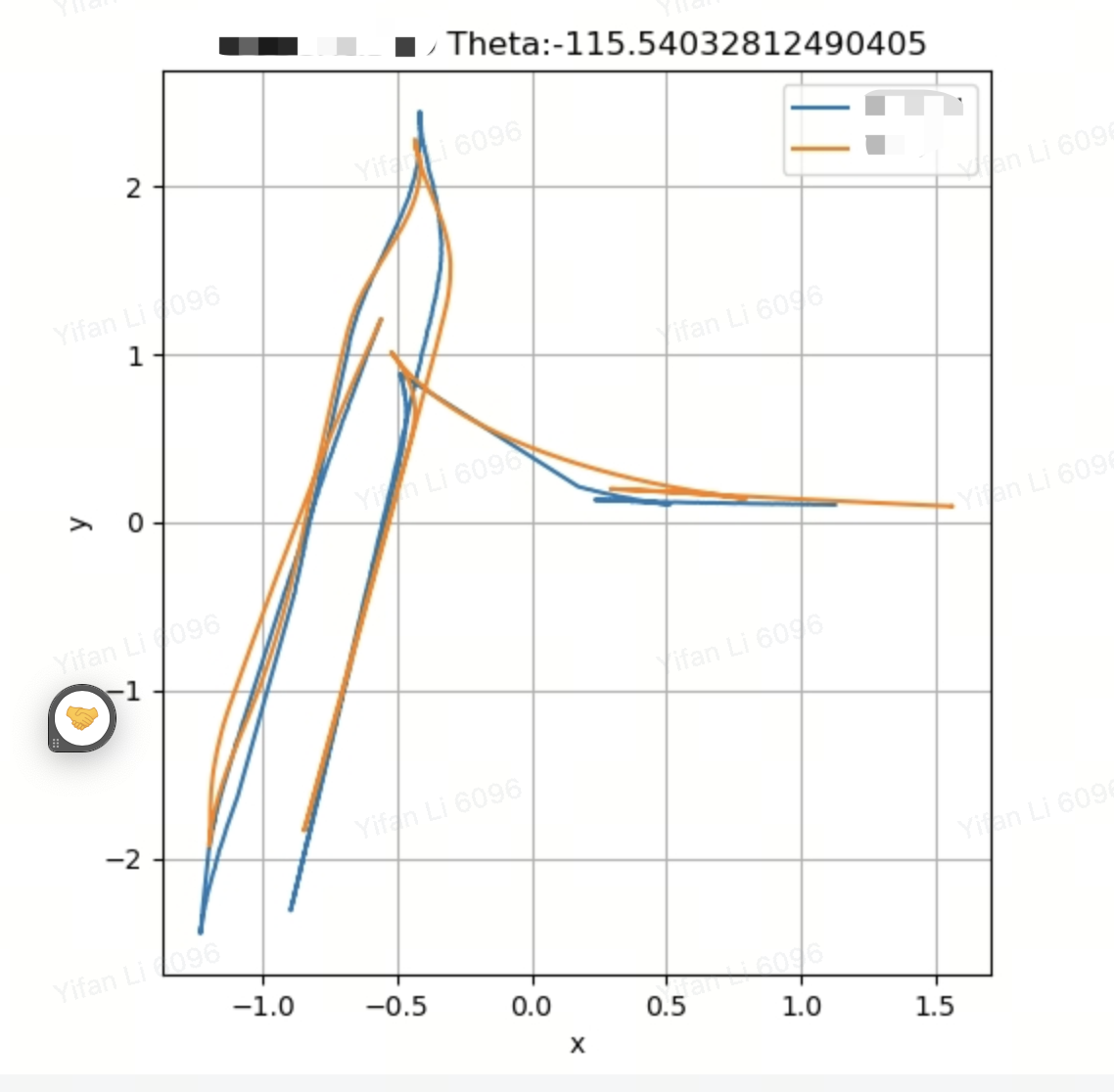
此時旋轉的角度確實如我們所想,度數120度左右,效果大概是這樣,看起來還不錯,那這樣的基礎上我們再去撰寫DTW演算法就速度比較快了,Python并沒有自帶的DTW(Dynamic Time Warping)演算法,但是第三方的庫,例如fastdtw和dtaidistance提供了這個演算法的實作,
使用fastdtw:
from scipy.spatial.distance import euclidean
from fastdtw import fastdtw
x = np.array([1, 2, 3, 4, 5], dtype=float)
y = np.array([2, 3, 4, 5, 6], dtype=float)
distance, path = fastdtw(x, y, dist=euclidean)
print("DTW distance: ", distance)
print("DTW path: ", path)
在上述代碼中,fastdtw函式接收兩個序列,x和y,以及一個用于計算兩點之間距離的函式,這里采用歐氏距離進行計算,
使用dtaidistance:
from dtaidistance import dtw
x = np.array([1, 2, 3, 4, 5], dtype=float)
y = np.array([2, 3, 4, 5, 6], dtype=float)
distance = dtw.distance(x, y)
print("DTW distance: ", distance)
在這段代碼中,dtw.distance函式接收兩個序列,并回傳它們之間的DTW距離,
# 對第二條曲線進行旋轉,并計算與第一條曲線的DTW距離
def compute_dtw_distance(points1, points2, angle, center_point):
rotated_points = rotate_points(points2, angle, center_point)
distance, _ = fastdtw(points1, rotated_points, dist=euclidean)
return distance
# 尋找最佳擬合角度
def find_best_fit(points1, points2, center_point=(0, 0), theta = 0):
"""Finds the rotation angle that gives the best fit between two sets of points."""
angles=np.arange(theta-10, theta+10, 0.3)
min_distance = float('inf')
best_angle = None
for angle in angles:
distance = compute_dtw_distance(points1, points2, angle, center_point)
if distance < min_distance:
min_distance = distance
best_angle = angle
return best_angle, min_distance
代碼里面我們為了減輕計算量,角度區間為之前得到的theta以及 正負10度,每隔0.3度進行一次計算,然后我們再根據得到的best_angle旋轉1次獲得最后的結果,
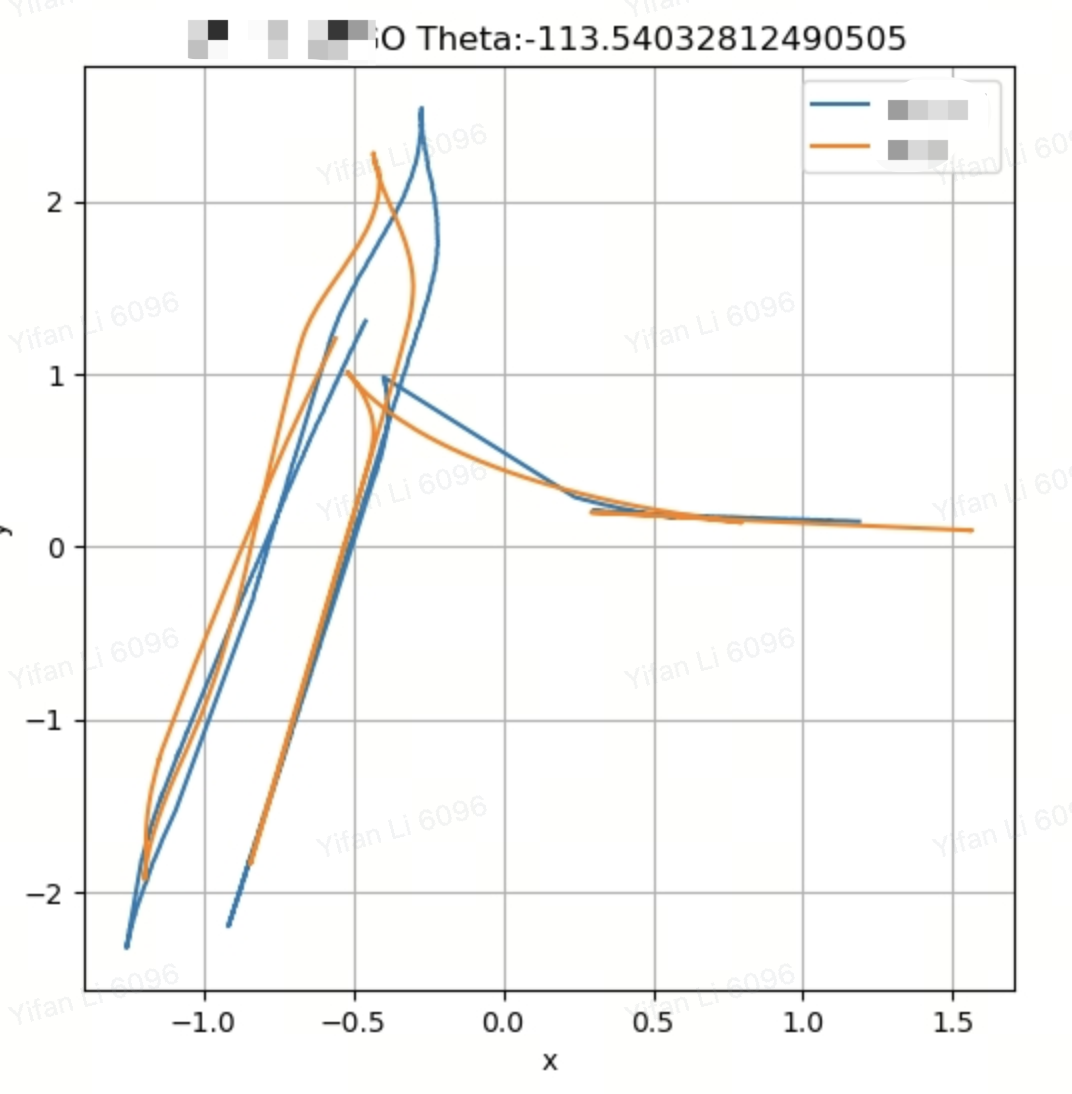
這樣一看,兩條線就非常的貼合了,角度也調整成了115.5度,但是老板突然跟我說有沒有可能這不是最貼合的情況(我#¥#@#@!#@$$#$@),要我把初始點不對齊也算一下,我想了一下,也做了幾組測驗,我選取了起點周圍情況0.4*0.4面積內的格點,一般情況也不會在這個范圍之外了,進行一個回圈的計算,保留做小的距離和最佳的角度
tran_x = EGO_xs[0] - BOSCH_xs[0]
tran_y = EGO_ys[0] - BOSCH_ys[0]
trans_x = np.linspace(tran_x-0.2, tran_x + 0.2, 5)
trans_y = np.linspace(tran_y-0.2, tran_y + 0.2, 5)
min_distance = float('inf')
best_angle = 0.0
best_bosch_x = []
best_bosch_y = []
start_time = time.time()
for i in trans_x:
for j in trans_y:
tmpx,tmpy = copy.deepcopy(BOSCH_xs), copy.deepcopy(BOSCH_ys)
tmpx,tmpy = translate_points(tmpx,tmpy, i, j)
ego = np.column_stack((EGO_xs, EGO_ys))
bosch = np.column_stack((tmpx,tmpy))
angle, distance = find_best_fit(ego,bosch,center_point=(tmpx[0],tmpy[0]),theta= theta)
if distance < min_distance:
min_distance = distance
best_angle = angle
best_bosch_x = tmpx
best_bosch_y = tmpy
print("此時Bosch的起點在{},{}, 平移的長度為{},{}".format(tmpx[0],tmpy[0],i,j))
print(BOSCH_xs[0], BOSCH_ys[0])
print("起點在{},{} 最佳角度為{} 誤差距離為{}".format(tmpx[0],tmpy[0],angle,distance))
BOSCH_xs, BOSCH_ys = rotate_points_after_DTW(best_bosch_x,best_bosch_y, best_angle)
別說,你還真別說,上圖所示的才是最擬合狀態,角度也有微小的變化,這是根據DTW演算法得出的結果,但是我個人覺得起點對齊的時候更擬合一點,~~~
全部代碼可以聯系本菜雞!純原創!!!
本文來自博客園,作者:ivanlee717,轉載請注明原文鏈接:https://www.cnblogs.com/ivanlee717/p/17547754.html
轉載請註明出處,本文鏈接:https://www.uj5u.com/qita/557138.html
標籤:其他
下一篇:返回列表
