影像恢復 Restormer: 徹底理解論文和源代碼 (注釋詳盡)

1. Restormer 論文

主要作業：
[1] MDTA (Multi-Dconv Head Transposed Attention), 聚合區域和非區域的像素互動，可以有效處理高解析度影像，
[2] GDFN (Gated-Dconv Feed-Forward Network), 控制特征轉換，抑制小資訊量的特征，僅允許有用的資訊進入下一次網路，
論文：https://arxiv.org/pdf/2111.09881.pdf
源代碼：
[1] https://github.com/swz30/Restormer
[2] https://download.csdn.net/download/Wenyuanbo/83592489
網路細節注釋和自定義訓練測驗代碼：https://download.csdn.net/download/Wenyuanbo/83617599

2. Restormer 網路結構

2.1 整體框架

論文的主要創新點是將經典 Transformer 中的 MSA 和 FFN 都進行改進，并且采用 Encoder-Decoder 架構，涉及的上采樣操作使用 nn.PixelShuffle() 來實作，涉及的下采樣操作使用 nn.PixelUnshuffle() 來實作，整體文章的脈絡非常清晰，

2.2 MDTA

與一般 Transformer 不同的是，論文在自注意力模板進行 token 計算時不是常見的 patch-wise，而是 pixel-wise，首先利用 11 卷積升維，再使用 33 分組卷積將特征分為三塊，最后進行經典的自注意力計算，

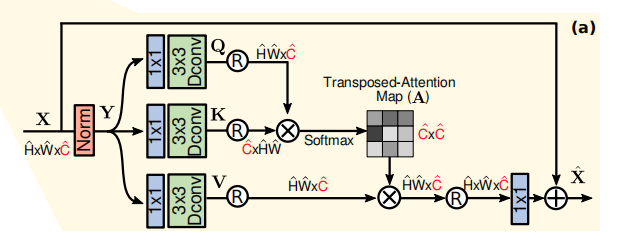
2.3 GDFN

論文提出雙路門控網路來取代 FFN，分別進行 11 升維，再利用 33 分組卷積提取特征，隨后使用 GELU 激活函式門控，最后 1*1 卷積降維輸出，

3. 主要代碼理解

3.1 MDTA

## Multi-DConv Head Transposed Self-Attention (MDTA)
class Attention(nn.Module):
    def __init__(self, dim, num_heads, bias):
        super(Attention, self).__init__()
        self.num_heads = num_heads  # 注意力頭的個數
        self.temperature = nn.Parameter(torch.ones(num_heads, 1, 1))  # 可學習系數
        
        # 1*1 升維
        self.qkv = nn.Conv2d(dim, dim*3, kernel_size=1, bias=bias)
        # 3*3 分組卷積
        self.qkv_dwconv = nn.Conv2d(dim*3, dim*3, kernel_size=3, stride=1, padding=1, groups=dim*3, bias=bias)
        # 1*1 卷積
        self.project_out = nn.Conv2d(dim, dim, kernel_size=1, bias=bias)

    def forward(self, x):
        b,c,h,w = x.shape  # 輸入的結構 batch 數，通道數和高寬

        qkv = self.qkv_dwconv(self.qkv(x))
        q,k,v = qkv.chunk(3, dim=1)  #  第 1 個維度方向切分成 3 塊
        # 改變 q, k, v 的結構為 b head c (h w)，將每個二維 plane 展平
        q = rearrange(q, 'b (head c) h w -> b head c (h w)', head=self.num_heads)
        k = rearrange(k, 'b (head c) h w -> b head c (h w)', head=self.num_heads)
        v = rearrange(v, 'b (head c) h w -> b head c (h w)', head=self.num_heads)

        q = torch.nn.functional.normalize(q, dim=-1)  # C 維度標準化，這里的 C 與通道維度略有不同
        k = torch.nn.functional.normalize(k, dim=-1)

        attn = (q @ k.transpose(-2, -1)) * self.temperature
        attn = attn.softmax(dim=-1)

        out = (attn @ v)  # 注意力圖(嚴格來說不算圖)
        
        # 將展平后的注意力圖恢復
        out = rearrange(out, 'b head c (h w) -> b (head c) h w', head=self.num_heads, h=h, w=w)
        # 真正的注意力圖
        out = self.project_out(out)
        return out

3.2 GDFN

## Gated-Dconv Feed-Forward Network (GDFN)
class FeedForward(nn.Module):
    def __init__(self, dim, ffn_expansion_factor, bias):
        super(FeedForward, self).__init__()
        
        # 隱藏層特征維度等于輸入維度乘以擴張因子
        hidden_features = int(dim*ffn_expansion_factor)
        # 1*1 升維
        self.project_in = nn.Conv2d(dim, hidden_features*2, kernel_size=1, bias=bias)
        # 3*3 分組卷積
        self.dwconv = nn.Conv2d(hidden_features*2, hidden_features*2, kernel_size=3, stride=1, padding=1, groups=hidden_features*2, bias=bias)
        # 1*1 降維
        self.project_out = nn.Conv2d(hidden_features, dim, kernel_size=1, bias=bias)

    def forward(self, x):
        x = self.project_in(x)
        x1, x2 = self.dwconv(x).chunk(2, dim=1)  # 第 1 個維度方向切分成 2 塊
        x = F.gelu(x1) * x2  # gelu 相當于 relu+dropout
        x = self.project_out(x)
        return x

3.3 TransformerBlock

## 就是標準的 Transformer 架構
class TransformerBlock(nn.Module):
    def __init__(self, dim, num_heads, ffn_expansion_factor, bias, LayerNorm_type):
        super(TransformerBlock, self).__init__()

        self.norm1 = LayerNorm(dim, LayerNorm_type)  # 層標準化
        self.attn = Attention(dim, num_heads, bias)  # 自注意力
        self.norm2 = LayerNorm(dim, LayerNorm_type)  # 層表轉化
        self.ffn = FeedForward(dim, ffn_expansion_factor, bias)  # FFN

    def forward(self, x):
        x = x + self.attn(self.norm1(x))  # 殘差
        x = x + self.ffn(self.norm2(x))  # 殘差

        return x

3.4 一個測驗實體

model = Restormer()
print(model)  # 列印網路結構

x = torch.randn((1, 3, 64, 64))  #隨機生成輸入影像
x = model(x)  # 送入網路
print(x.shape) # 列印網路輸入的影像結構

參考文獻

[1] Zamir S W, Arora A, Khan S, et al. Restormer: Efficient Transformer for High-Resolution Image Restoration[J]. arXiv preprint arXiv:2111.09881, 2021.
[2] 中國海洋大學AI前沿理論組. 【ARXIV2111】Restormer: Efficient Transformer for High-Resolution Image Restoration.

結語與思考

1. 實驗證明 Restormer 在影像去雨、影像去模糊、影像去噪等任務上都取得了相當不錯的表現，但是論文沒有與別的演算法進行引數和效率的對比，據我所知 MPRNet 的引數量為 3.64 M，而 Restormer 是 25.3 M，如果靠堆引數量和燒錢使結果 SOTA 那我等小組就只能望而卻步了，
2. 在 GDFN 中存在一個擴展因子 γ = 2.66 \gamma=2.66 γ=2.66 ，論文對其的解釋很簡單，就是為了使網路引數和計算負擔與一般 FFN 一致，
3. 完整的注釋和自定義訓練測驗代碼請移步：https://download.csdn.net/download/Wenyuanbo/83617599