主頁 > 後端開發 > 【調制解調】VSB 殘留邊帶調幅

【調制解調】VSB 殘留邊帶調幅

2023-07-13 08:46:20 後端開發

說明

學習數字信號處理演算法時整理的學習筆記，同系列文章目錄可見 《DSP 學習之路》目錄，代碼已上傳到 Github - ModulationAndDemodulation，本篇介紹 VSB 殘留邊帶調幅信號的調制與解調，內附全套 MATLAB 代碼，

目錄
  • 說明
  • 1. VSB 調制演算法
    • 1.1 演算法描述
    • 1.2 濾波法 VSB 信號調制示例
  • 2. VSB 解調演算法
    • 2.1 插入載波包絡檢波法
    • 2.2 相干解調（同步檢測）
  • 參考資料
  • 附錄代碼
    • 附.1 檔案 lpf_filter.m
    • 附.2 檔案 vsblpf_filter.m
    • 附.3 檔案 vsbhpf_filter.m
    • 附.4 檔案 mod_lvsb.m
    • 附.5 檔案 mod_uvsb.m
    • 附.6 檔案 main_modVSB_example.m
    • 附.7 檔案 demod_vsb_method1.m
    • 附.8 檔案 demod_vsb_method2.m
    • 附.9 檔案 main_demodVSB_example1.m
    • 附.10 檔案 main_demodVSB_example2.m


1. VSB 調制演算法

1.1 演算法描述

殘留邊帶調制（VSB, Vestigial Side Band）是介于 SSB 與 DSB 之間的一種折中方式，它既克服了 DSB 信號占用頻帶寬的缺點，又解決了 SSB 信號實作中的困難（無法在工程上實作理想濾波器以及精準相移），在這種調制方式中，不像 SSB 中那樣完全抑制 DSB 信號的一個邊帶，而是逐漸切割，使其殘留一小部分，VSB 信號的帶寬略大于基帶信號（調制信號）帶寬 \(f_H\)，但小于 DSB 信號的帶寬，即 \({f_H}<{B_{VSB}}<2{f_H}\)，

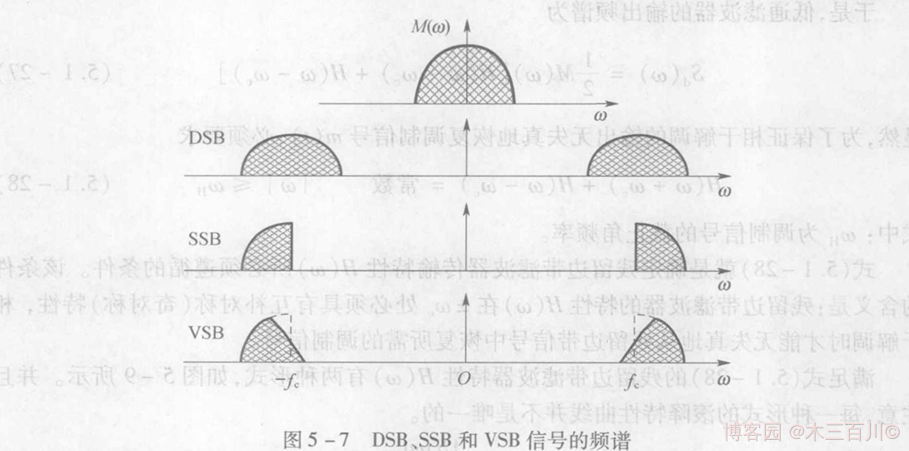
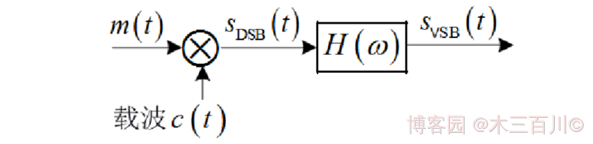
Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

用濾波法產生 VSB 信號的方法與 SSB 信號大致相同，都是先產生一個雙邊帶 DSB 信號，然后讓其通過一個殘留邊帶濾波器（這個濾波器在 \(\pm{\omega_c}\) 處必須具有互補對稱性），即可得到單邊帶 SSB 信號，

Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

為了保證相干解調時無失真地從殘留邊帶信號中恢復所需的調制信號，殘留邊帶濾波器的頻譜必須滿足：

\[H({\omega}+{\omega_c})+H({\omega}-{\omega_c})=常數, {\lvert}{\omega}{\rvert} \leq {\omega_H} \tag{1} \]

式中，\(\omega_H\) 為調制信號的截止角頻率，這個條件的幾何含義是：殘留邊帶濾波器 \(H(\omega)\) 在 \(\pm{\omega_c}\) 處必須具有互補對稱（奇對稱）特性，即濾波器有過渡帶，其中一個邊帶損失的恰好能夠被另外一個邊帶殘留的部分補償，滿足式 \((1)\) 的殘留邊帶濾波器 \(H(\omega)\) 有以下兩種形式，并且注意，每一種形式的滾降特性曲線并不是唯一的，下圖 \((a)\) 是殘留小部分上邊帶的濾波器特性，下圖 \((b)\) 是殘留小部分下邊帶的濾波器特性，

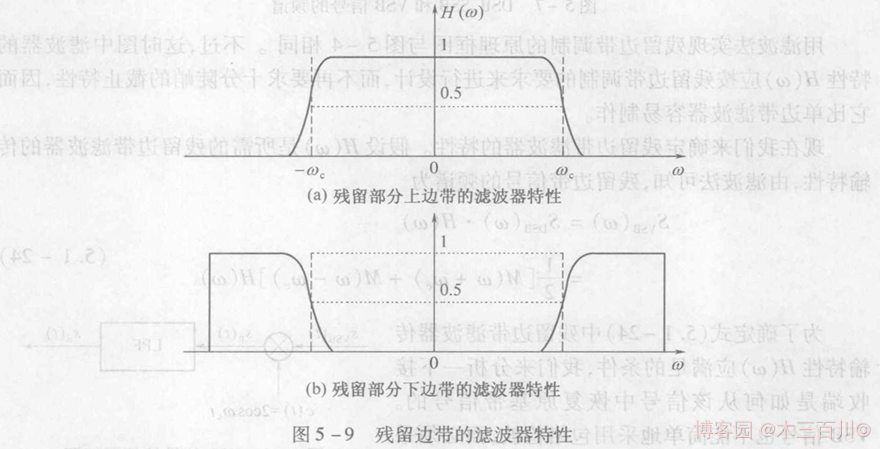
Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

1.2 濾波法 VSB 信號調制示例

調制信號 \(m(t)\) 可以是確知信號，也可以是隨機信號，當 \(m(t)\) 是確知信號時，不妨假設 \(m(t)\) 的時域運算式如下：

\[m(t) = sin(2{\pi}{f_m}t)+cos({\pi}{f_m}t) \tag{2} \]

各調制引數取值：\(f_m=2500Hz\)，\(f_c=20000Hz\)，信號采樣率 \(f_s=8{f_c}\)，仿真總時長為 \(2s\)，假設殘留濾波器的滾降特性曲線為直線，VSB 殘留下邊帶調制效果如下圖所示（為了美觀，時域只顯示前 500 個點），調制信號 \(m(t)\) 雙邊幅度譜有四根離散譜線（\({\pm}2500Hz\)、\({\pm}1250Hz\)），高頻載波 \(c(t)\) 雙邊幅度譜有兩根離散譜線（\({\pm}20000Hz\)），VSB 殘留下邊帶信號有六根離散譜線（\(\pm18750Hz\)、\(\pm21250Hz\)、\(\pm22500Hz\)），

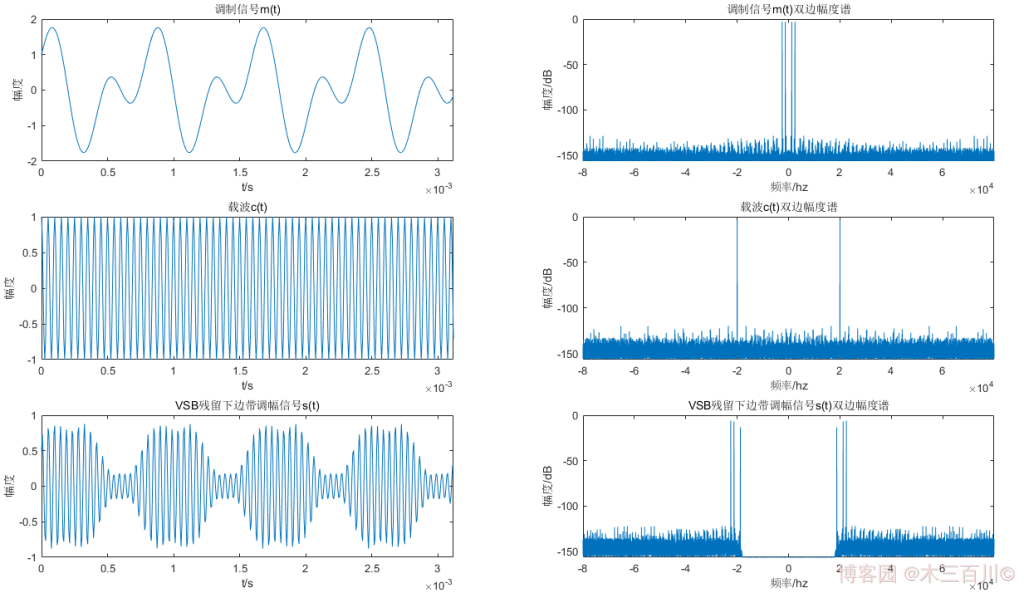
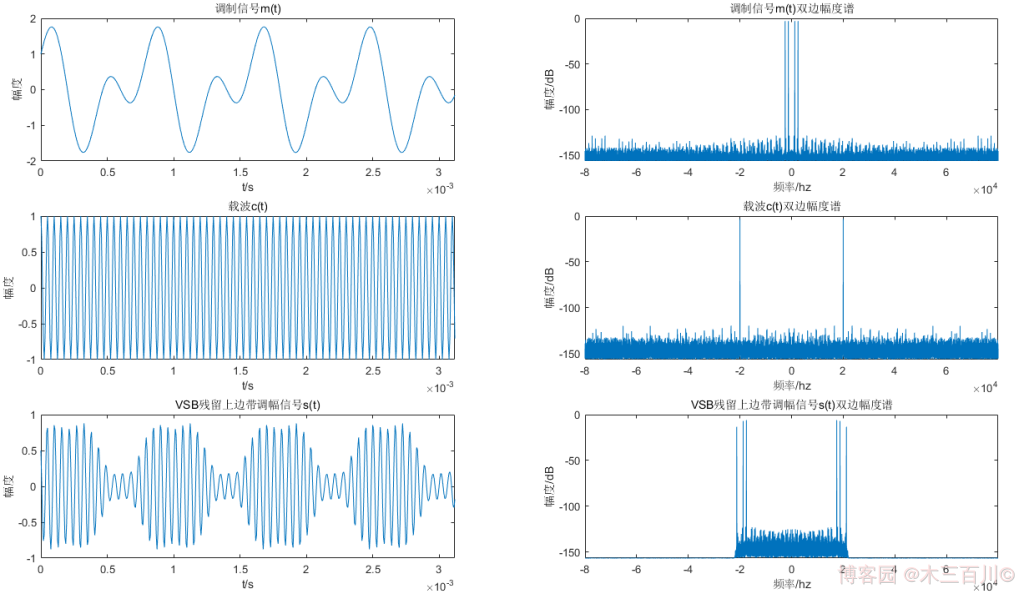
Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

VSB 殘留上邊帶調制效果如下圖所示（為了美觀，時域只顯示前 500 個點），調制信號 \(m(t)\) 雙邊幅度譜有四根離散譜線（\({\pm}2500Hz\)、\({\pm}1250Hz\)），高頻載波 \(c(t)\) 雙邊幅度譜有兩根離散譜線（\({\pm}20000Hz\)），VSB 殘留上邊帶信號有六根離散譜線（\(\pm17500Hz\)、\(\pm18750Hz\)、\(\pm21250Hz\)），

Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

代碼詳見 mod_lvsb.m、mod_uvsb.m、main_modVSB_example.m，


2. VSB 解調演算法

解調是調制的逆程序，其作用是從接收的已調信號中恢復原基帶信號（即調制信號），VSB 信號的包絡不再與調制信號 \(m(t)\) 的變化規律一致，因而不能采用簡單的包絡檢波來恢復調制信號，通常采用相干解調的方法來進行解調，另一種方法是，插入很強的載波，使其成為或近似為 AM 信號，則可利用包絡檢波器恢復調制信號，這種方法被稱為插入載波包絡檢波法，為了保證檢波質量，插入的載波振幅應遠大于信號的振幅，同時也要求插入的載波與調制載波同頻同相，下面介紹兩種解調方法并對 1.2 節中的 VSB 信號進行解調，

2.1 插入載波包絡檢波法

插入幅值為 \(A_0\) 的載波，得到一個近似的 AM 信號，使用 AM 解調器進行解調即可，步驟如下：

  1. 第一步：加上載波 \({A_0}cos{\omega_ct}\)，其中 \(A_0 \geq {\lvert}{s_{VSB}(t)}{\rvert}_{max}\)，獲得 AM 信號，
  2. 第二步：使用 AM 解調器進行解調，

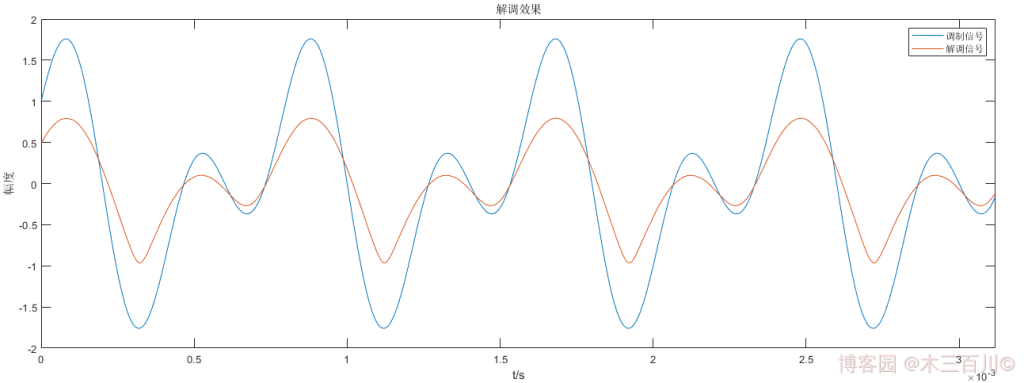
對 1.2 節中的 VSB 殘留下邊帶信號，設定信噪比 \(SNR=50dB\)，解調效果如下，解調后幅度放大系數 \(k=\overline{{\lvert}m(t){\rvert}}/\overline{{\lvert}\hat{m}(t){\rvert}}\approx2.12\)，使用這個系數放大解調信號幅值，然后計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-k\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.1769\)，

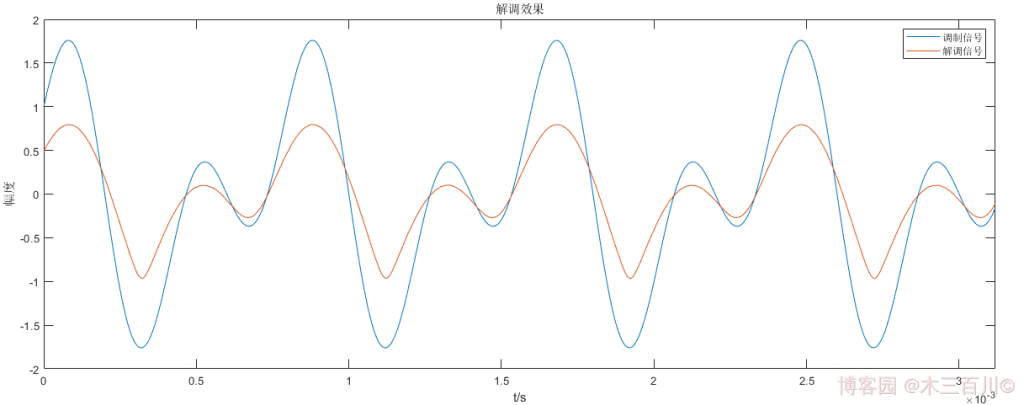
Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

對 1.2 節中的 VSB 殘留上邊帶信號，設定信噪比 \(SNR=50dB\)，解調效果如下，解調后幅度放大系數 \(k=\overline{{\lvert}m(t){\rvert}}/\overline{{\lvert}\hat{m}(t){\rvert}}\approx2.12\)，使用這個系數放大解調信號幅值，然后計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-k\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.1768\)，與 VSB 殘留下邊帶信號相同，

Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

代碼詳見 demod_vsb_method1.m 和 main_demodVSB_example1.m，AM 解調器詳見本人同系列博客 【調制解調】AM 調幅，更改插入載波的初始相位為 \({\phi_0}=\pi/4,\pi/2\)，或者更改插入載波的中心頻率為 \(0.8f_c,1.2f_c\) 后，解調效果變差，說明這種方法對插入載波同頻同相的要求較高，

2.2 相干解調（同步檢測）

將 VSB 信號與同頻同相的相干載波相乘，然后通過一個低通濾波器即可獲得解調結果，步驟如下：

  1. 第一步：乘以相干載波（即乘以 \(4cos({\omega_ct}+{\phi_0})\)，前面的 4 被用來做幅度補償，
  2. 第二步：低通濾波器濾除高頻載波，濾除 \(2{\omega}_c\)，

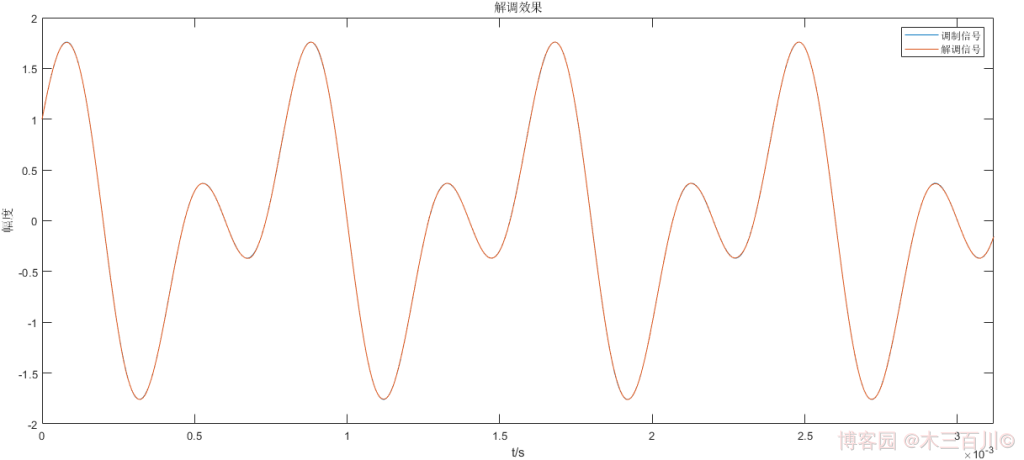
對 1.2 節中的 VSB 殘留下邊帶信號，設定信噪比 \(SNR=50dB\)，解調效果如下，計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0021\)，

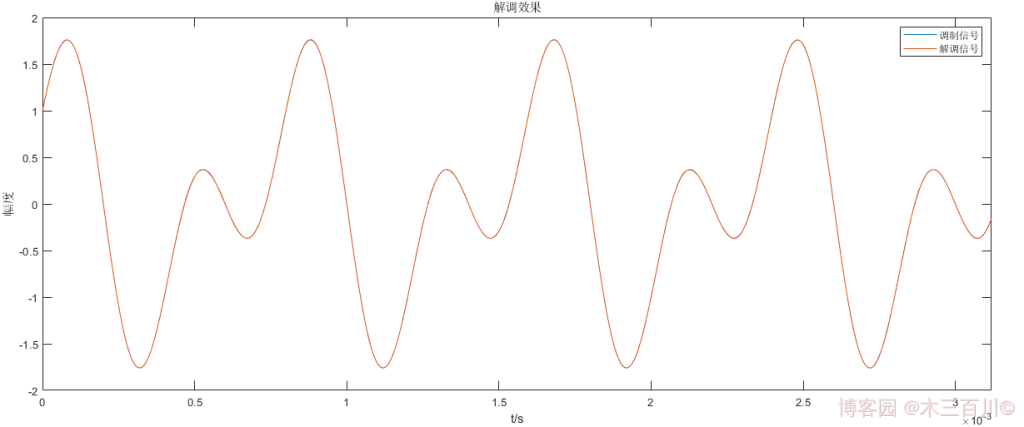
Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

對 1.2 節中的 VSB 殘留上邊帶信號，設定信噪比 \(SNR=50dB\)，解調效果如下，計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0021\)，與 VSB 殘留下邊帶信號相同，

Oh Shit!-圖片走丟了-打個廣告-歡迎來博客園關注“木三百川”

代碼詳見 demod_vsb_method2.m 和 main_demodVSB_example2.m，更改相干載波的初始相位為 \({\phi_0}=\pi/4,\pi/2\)，或者更改相干載波的中心頻率為 \(0.8f_c,1.2f_c\) 后，解調效果變差，說明這種方法對相干載波同頻同相的要求也較高，


參考資料

[1] 樓才義,徐建良,楊小牛.軟體無線電原理與應用[M].電子工業出版社,2014.

[2] 樊昌信,曹麗娜.通信原理.第7版[M].國防工業出版社,2012.

[3] 人人文庫 - 殘留邊帶 VSB 的調制與解調實用教案，

[4] 百度文庫 - 殘留邊帶的調制與解調PPT，


附錄代碼

附.1 檔案 lpf_filter.m

function sig_lpf = lpf_filter(sig_data, cutfre)
% LPF_FILTER    自定義理想低通濾波器
% 輸入引數：
%       sig_data        待濾波資料
%       cutfre          截止頻率，范圍 (0,1)
% 輸出引數：
%       sig_lpf         低通濾波結果
% @author 木三百川

nfft = length(sig_data);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
sig_fft_lpf = fftshift(fft(sig_data));
sig_fft_lpf([1:lidx,ridx:nfft]) = 0;
sig_lpf = real(ifft(fftshift(sig_fft_lpf)));

end

附.2 檔案 vsblpf_filter.m

function sig_lpf = vsblpf_filter(sig_data, cutfre, cutband)
% VSBLPF_FILTER    自定義殘留邊帶低通濾波器(滾降特性曲線為直線)
% 輸入引數：
%       sig_data        待濾波資料
%       cutfre          截止頻率，范圍 (0,1)
%       cutband         殘留寬度，范圍 (0,2*cutfre)
% 輸出引數：
%       sig_lpf         低通濾波結果
% @author 木三百川

% 低通濾波器
nfft = length(sig_data);
widx = round(nfft*cutband/4);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
vsblpf = zeros(size(sig_data));
vsblpf(lidx-widx:lidx+widx) = linspace(0,1,2*widx+1);
vsblpf(lidx+widx:ridx-widx) = 1;
vsblpf(ridx-widx:ridx+widx) = linspace(1,0,2*widx+1);

% 濾波
sig_fft_lpf = fftshift(fft(sig_data)).*vsblpf;
sig_lpf = real(ifft(fftshift(sig_fft_lpf)));

end

附.3 檔案 vsbhpf_filter.m

function sig_hpf = vsbhpf_filter(sig_data, cutfre, cutband)
% VSBHPF_FILTER    自定義殘留邊帶高通濾波器(滾降特性曲線為直線)
% 輸入引數：
%       sig_data        待濾波資料
%       cutfre          截止頻率，范圍 (0,1)
%       cutband         殘留寬度，范圍 (0,2*cutfre)
% 輸出引數：
%       sig_hpf         高通濾波結果
% @author 木三百川

% 高通濾波器
nfft = length(sig_data);
widx = round(nfft*cutband/4);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
vsbhpf = ones(size(sig_data));
vsbhpf(lidx-widx:lidx+widx) = linspace(1,0,2*widx+1);
vsbhpf(lidx+widx:ridx-widx) = 0;
vsbhpf(ridx-widx:ridx+widx) = linspace(0,1,2*widx+1);

% 濾波
sig_fft_hpf = fftshift(fft(sig_data)).*vsbhpf;
sig_hpf = real(ifft(fftshift(sig_fft_hpf)));

end

附.4 檔案 mod_lvsb.m

function [ sig_lvsb ] = mod_lvsb(fc, fs, mt, t)
% MOD_LVSB        VSB 殘留邊帶調幅（濾波法，殘留小部分下邊帶）
% 輸入引數：
%       fc      載波中心頻率
%       fs      信號采樣率
%       mt      調制信號
%       t       采樣時間
% 輸出引數：
%       sig_lvsb VSB 殘留下邊帶調幅實信號
% @author 木三百川

% 生成DSB信號
ct = cos(2*pi*fc*t);  
sig_dsb = mt.*ct;   % DSB 雙邊帶調幅信號

% 濾波
sig_lvsb = vsbhpf_filter(sig_dsb, fc/(fs/2), 0.2*fc/(fs/2));

% 繪圖
nfft = length(sig_lvsb);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_lvsb));
subplot(3,2,1);
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('調制信號m(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('調制信號m(t)雙邊幅度譜');

subplot(3,2,3);
plot(t(1:plot_length), ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('載波c(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('載波c(t)雙邊幅度譜');

subplot(3,2,5);
plot(t(1:plot_length), sig_lvsb(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('VSB殘留下邊帶調幅信號s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_lvsb,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('VSB殘留下邊帶調幅信號s(t)雙邊幅度譜');

end

附.5 檔案 mod_uvsb.m

function [ sig_uvsb ] = mod_uvsb(fc, fs, mt, t)
% MOD_UVSB        VSB 殘留邊帶調幅（濾波法，殘留小部分上邊帶）
% 輸入引數：
%       fc      載波中心頻率
%       fs      信號采樣率
%       mt      調制信號
%       t       采樣時間
% 輸出引數：
%       sig_uvsb VSB 殘留上邊帶調幅實信號
% @author 木三百川

% 生成DSB信號
ct = cos(2*pi*fc*t);  
sig_dsb = mt.*ct;   % DSB 雙邊帶調幅信號

% 濾波
sig_uvsb = vsblpf_filter(sig_dsb, fc/(fs/2), 0.2*fc/(fs/2));

% 繪圖
nfft = length(sig_uvsb);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_uvsb));
subplot(3,2,1);
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('調制信號m(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('調制信號m(t)雙邊幅度譜');

subplot(3,2,3);
plot(t(1:plot_length), ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('載波c(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('載波c(t)雙邊幅度譜');

subplot(3,2,5);
plot(t(1:plot_length), sig_uvsb(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('VSB殘留上邊帶調幅信號s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_uvsb,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('VSB殘留上邊帶調幅信號s(t)雙邊幅度譜');

end

附.6 檔案 main_modVSB_example.m

clc;
clear;
close all;
% VSB 調制仿真(調制信號為確知信號)
% @author 木三百川

% 調制引數
fm = 2500;              % 調制信號引數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 采樣率
total_time = 2;         % 仿真時長，單位：秒

% 采樣時間
t = 0:1/fs:total_time-1/fs;

% 調制信號為確知信號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% VSB 調制
[ sig_lvsb ] = mod_lvsb(fc, fs, mt, t); % 殘留下邊帶
[ sig_uvsb ] = mod_uvsb(fc, fs, mt, t); % 殘留上邊帶

附.7 檔案 demod_vsb_method1.m

function [ sig_vsb_demod ] = demod_vsb_method1(sig_vsb_receive, fc, fs, t, phi0)
% DEMOD_VSB_METHOD1        VSB 插入載波包絡檢波法
% 輸入引數：
%       sig_vsb_receive     VSB 接收信號，行向量
%       fc                  載波中心頻率
%       fs                  信號采樣率
%       t                   采樣時間
%       phi0                載波初始相位
% 輸出引數：
%       sig_vsb_demod       解調結果，與 sig_vsb_receive 等長
% @author 木三百川

% 第一步：插入載波
A0 = max(abs(sig_vsb_receive))/0.8;
sig_vsb2am = sig_vsb_receive + A0*cos(2*pi*fc*t+phi0);

% 第二步：使用 AM 解調器進行解調
[ sig_vsb_demod ] = demod_am_method4(sig_vsb2am, fs, t);

end

附.8 檔案 demod_vsb_method2.m

function [ sig_vsb_demod ] = demod_vsb_method2(sig_vsb_receive, fc, fs, t, phi0)
% DEMOD_VSB_METHOD2        VSB 相干解調（同步檢測）
% 輸入引數：
%       sig_vsb_receive     VSB 接收信號，行向量
%       fc                  載波中心頻率
%       fs                  信號采樣率
%       t                   采樣時間
%       phi0                載波初始相位
% 輸出引數：
%       sig_vsb_demod       解調結果，與 sig_vsb_receive 等長
% @author 木三百川

% 第一步：乘以相干載波
sig_vsbct = 4*sig_vsb_receive.*cos(2*pi*fc*t+phi0);

% 第二步：低通濾波
sig_vsb_demod = lpf_filter(sig_vsbct, fc/(fs/2));

end

附.9 檔案 main_demodVSB_example1.m

clc;
clear;
close all;
% VSB 解調仿真(調制信號為確知信號，插入載波包絡檢波法)
% @author 木三百川

% 調制引數
fm = 2500;              % 調制信號引數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 采樣率
total_time = 2;         % 仿真時長，單位：秒

% 采樣時間
t = 0:1/fs:total_time-1/fs;

% 調制信號為確知信號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% VSB 調制
% [ sig_vsb_send ] = mod_lvsb(fc, fs, mt, t);  % 殘留下邊帶
[ sig_vsb_send ] = mod_uvsb(fc, fs, mt, t);  % 殘留上邊帶

% 加噪聲
snr = 50;               % 信噪比
sig_vsb_receive = awgn(sig_vsb_send, snr, 'measured');

% 插入載波包絡檢波法
phi0 = 0;
[ sig_vsb_demod ] = demod_vsb_method1(sig_vsb_receive, fc, fs, t, phi0);

% 繪圖
nfft = length(sig_vsb_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_vsb_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_vsb_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('VSB接收信號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_vsb_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('VSB接收信號雙邊幅度譜');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_vsb_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調制信號','解調信號');

coef = mean(abs(mt))/mean(abs(sig_vsb_demod));
fprintf('norm(調制信號 - %.2f * 解調信號)/norm(調制信號) = %.4f.\n', coef, norm(mt-coef*sig_vsb_demod)/norm(mt));

附.10 檔案 main_demodVSB_example2.m

clc;
clear;
close all;
% VSB 解調仿真(調制信號為確知信號，相干解調（同步檢測）)
% @author 木三百川

% 調制引數
fm = 2500;              % 調制信號引數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 采樣率
total_time = 2;         % 仿真時長，單位：秒

% 采樣時間
t = 0:1/fs:total_time-1/fs;

% 調制信號為確知信號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% VSB 調制
[ sig_vsb_send ] = mod_lvsb(fc, fs, mt, t);  % 殘留下邊帶
% [ sig_vsb_send ] = mod_uvsb(fc, fs, mt, t);  % 殘留上邊帶

% 加噪聲
snr = 50;               % 信噪比
sig_vsb_receive = awgn(sig_vsb_send, snr, 'measured');

% 相干解調（同步檢測）
phi0 = 0;
[ sig_vsb_demod ] = demod_vsb_method2(sig_vsb_receive, fc, fs, t, phi0);

% 繪圖
nfft = length(sig_vsb_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_vsb_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_vsb_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('VSB接收信號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_vsb_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('VSB接收信號雙邊幅度譜');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_vsb_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調制信號','解調信號');

coef = mean(abs(mt))/mean(abs(sig_vsb_demod));
fprintf('norm(調制信號 - %.2f * 解調信號)/norm(調制信號) = %.4f.\n', coef, norm(mt-coef*sig_vsb_demod)/norm(mt));

本文作者：木三百川

本文鏈接：https://www.cnblogs.com/young520/p/17549376.html

著作權宣告：本文系博主原創文章，著作權歸作者所有，商業轉載請聯系作者獲得授權，非商業轉載請附上出處鏈接，遵循 署名-非商業性使用-相同方式共享 4.0 國際版 (CC BY-NC-SA 4.0) 著作權協議，

轉載請註明出處，本文鏈接：https://www.uj5u.com/houduan/557186.html

標籤：其他

上一篇：【微服務學習1--組件】服務注冊中心--Eureka

下一篇：返回列表

標籤雲
其他(162507) Python(38275) JavaScript(25532) Java(18295) C(15242) 區塊鏈(8275) C＃(7972) AI(7469) 爪哇(7425) MySQL(7299) html(6777) 基礎類(6313) sql(6102) 熊猫(6058) PHP(5876) 数组(5741) R(5409) Linux(5347) 反应(5209) 腳本語言(PerlPython)(5129) 非技術區(4971) Android(4616) 数据框(4311) css(4259) 节点.js(4032) C語言(3288) json(3245) 列表(3129) 扑(3119) C++語言(3117) 安卓(2998) 打字稿(2995) VBA(2789) Java相關(2746) 疑難問題(2699) 细绳(2522) 單片機工控(2479) iOS(2439) ASP.NET(2404) MongoDB(2323) 麻木的(2285) 正则表达式(2254) 字典(2211) 循环(2198) 迅速(2185) 擅长(2169) 镖(2155) HtmlCss(2002) .NET技术(1988) 功能(1967) Web開發(1951) C++(1942) python-3.x(1918) 弹簧靴(1913) xml(1889) PostgreSQL(1884) .NETCore(1863) 谷歌表格(1846) Unity3D(1843) for循环(1842)

熱門瀏覽
  • 【C++】Microsoft C++、C 和匯編程式檔案

    ......

    uj5u.com 2020-09-10 00:57:23 more
  • 例外宣告

    相比于斷言適用于排除邏輯上不可能存在的狀態，例外通常是用于邏輯上可能發生的錯誤。 例外宣告 Item 1：當函式不可能拋出例外或不能接受拋出例外時，使用noexcept 理由 如果不打算拋出例外的話，程式就會認為無法處理這種錯誤，并且應當盡早終止，如此可以有效地阻止例外的傳播與擴散。 示例 //不可 ......

    uj5u.com 2020-09-10 00:57:27 more
  • Codeforces 1400E Clear the Multiset(貪心 + 分治)

    鏈接：https://codeforces.com/problemset/problem/1400/E 來源：Codeforces 思路：給你一個陣列，現在你可以進行兩種操作，操作1：將一段沒有 0 的區間進行減一的操作，操作2：將 i 位置上的元素歸零。最終問：將這個陣列的全部元素歸零后操作的最少 ......

    uj5u.com 2020-09-10 00:57:30 more
  • UVA11610 【Reverse Prime】

    本人看到此題沒有翻譯，就附帶了一個自己的翻譯版本 思考 這一題，它的第一個要求是找出所有 $7$ 位反向質數及其質因數的個數。 我們應該需要質數篩篩選1~$10^{7}$的所有數，這里就不慢慢介紹了。但是，重讀題，我們突然發現反向質數都是 $7$ 位，而將它反過來后的數字卻是 $6$ 位數，這就說明 ......

    uj5u.com 2020-09-10 00:57:36 more
  • 統計區間素數數量

    1 #pragma GCC optimize(2) 2 #include <bits/stdc++.h> 3 using namespace std; 4 bool isprime[1000000010]; 5 vector<int> prime; 6 inline int getlist(int ......

    uj5u.com 2020-09-10 00:57:47 more
  • C/C++編程筆記：C++中的 const 變數詳解，教你正確認識const用法

    1、C中的const 1、區域const變數存放在堆疊區中，會分配記憶體（也就是說可以通過地址間接修改變數的值）。測驗代碼如下： 運行結果： 2、全域const變數存放在只讀資料段（不能通過地址修改，會發生寫入錯誤）， 默認為外部聯編，可以給其他源檔案使用（需要用extern關鍵字修飾） 運行結果： ......

    uj5u.com 2020-09-10 00:58:04 more
  • 【C++犯錯記錄】VS2019 MFC添加資源不懂如何修改資源宏ID

    1. 首先在資源視圖中，添加資源 2. 點擊新添加的資源，復制自動生成的ID 3. 在解決方案資源管理器中找到Resource.h檔案，編輯，使用整個專案搜索和替換的方式快速替換 宏宣告 4. Ctrl+Shift+F 全域搜索，點擊查找全部，然后逐個替換 5. 為什么使用搜索替換而不使用屬性視窗直 ......

    uj5u.com 2020-09-10 00:59:11 more
  • 【C++犯錯記錄】VS2019 MFC不懂的批量添加資源

    1. 打開資源頭檔案Resource.h，在其中預先定義好宏 ID（不清楚其實ID值應該設定多少，可以先新建一個相同的資源項，再在這個資源的ID值的基礎上遞增即可） 2. 在資源視圖中選中專案資源，按F7編輯資源檔案，按 ID 型別 相對路徑的形式添加 資源。（別忘了先把檔案拷貝到專案中的res檔案 ......

    uj5u.com 2020-09-10 01:00:19 more
  • C/C++編程筆記：關于C++的參考型別，專供新手入門使用

    今天要講的是C++中我最喜歡的一個用法——參考，也叫別名。 參考就是給一個變數名取一個變數名，方便我們間接地使用這個變數。我們可以給一個變數創建N個參考，這N + 1個變數共享了同一塊記憶體區域。(參考型別的變數會占用記憶體空間，占用的記憶體空間的大小和指標型別的大小是相同的。雖然參考是一個物件的別名，但 ......

    uj5u.com 2020-09-10 01:00:22 more
  • 【C/C++編程筆記】從頭開始學習C ++：初學者完整指南

    眾所周知，C ++的學習曲線陡峭，但是花時間學習這種語言將為您的職業帶來奇跡，并使您與其他開發人員區分開。您會更輕松地學習新語言，形成真正的解決問題的技能，并在編程的基礎上打下堅實的基礎。 C ++將幫助您養成良好的編程習慣（即清晰一致的編碼風格，在撰寫代碼時注釋代碼，并限制類內部的可見性），并且由 ......

    uj5u.com 2020-09-10 01:00:41 more
最新发布
  • 【調制解調】VSB 殘留邊帶調幅

    學習數字信號處理演算法時整理的學習筆記。本篇介紹 VSB 殘留邊帶調幅信號的調制與解調，內附全套 MATLAB 代碼。 ......

    uj5u.com 2023-07-13 08:46:20 more
  • 【微服務學習1--組件】服務注冊中心--Eureka

    一、簡介： Eureka是由Netflix公司開源的一款提供服務注冊和發現的產品。因此，在添加依賴時，會有NetFlix。 該組件管理各種的服務功能：注冊、 發現、熔斷、負載、降級等。 Eureka采用的是基于C/S的設計架構。 Eureka由兩部分組成（Server/Client）：Eureka服 ......

    uj5u.com 2023-07-13 08:46:06 more
  • Python中實作定時任務

    # Python中實作定時任務 在專案中，我們可能遇到有定時任務的需求。 - 其一：每隔一個時間段就執行任務。 比如：壓測中每隔45分鐘調整溫箱的溫度。 - 其二：定時執行任務。 例如每天早上 8 點定時推送早報。 今天，我跟大家分享下 Python 定時任務的實作方法。 ## 固定時間間隔執行任務 ......

    uj5u.com 2023-07-13 08:45:57 more
  • Python中實作定時任務

    # Python中實作定時任務 在專案中，我們可能遇到有定時任務的需求。 - 其一：每隔一個時間段就執行任務。 比如：壓測中每隔45分鐘調整溫箱的溫度。 - 其二：定時執行任務。 例如每天早上 8 點定時推送早報。 今天，我跟大家分享下 Python 定時任務的實作方法。 ## 固定時間間隔執行任務 ......

    uj5u.com 2023-07-13 08:45:20 more
  • 【微服務學習1--組件】服務注冊中心--Eureka

    一、簡介： Eureka是由Netflix公司開源的一款提供服務注冊和發現的產品。因此，在添加依賴時，會有NetFlix。 該組件管理各種的服務功能：注冊、 發現、熔斷、負載、降級等。 Eureka采用的是基于C/S的設計架構。 Eureka由兩部分組成（Server/Client）：Eureka服 ......

    uj5u.com 2023-07-13 08:39:42 more
  • 一文了解io包中的discard型別

    # 1. 引言 `io.discard`是Go語言標準庫提供一個結構體型別，其在丟棄不需要的資料場景下非常好用。本文我們將從`io.discard` 型別的基本定義出發，講述其基本使用和實作原理，接著簡單描述 `io.discard` 的使用場景，基于此完成對 `io.discard` 型別的介紹。 ......

    uj5u.com 2023-07-13 07:58:18 more
  • [滲透測驗]—2.4 加密和解密技術

    在本節中，我們將介紹加密和解密技術的基礎知識，以及一些常見的加密演算法。我們將涵蓋以下主題： 1. 加密和解密的基本概念 2. 對稱加密 3. 非對稱加密 4. 哈希函式 5. 數字簽名 6. 實際應用及案例代碼 ### 1. 加密和解密的基本概念 - **加密**：加密是一種將資料（明文）轉換為其他 ......

    uj5u.com 2023-07-13 07:53:04 more
  • Java 封裝

    # Java 封裝 # 1. 封裝 ## 封裝就是把抽象的資料和方法進行封裝，資料在內部通過授權的方法來進行資料的操作，例如遙控器通過按鈕對電視機的操作。 ## 封裝的好處： > ## 隱藏實作細節 > > ## 校驗并保護資料的安全 ## 封裝的三步驟： > ## 對屬性進行私有化 > > ## ......

    uj5u.com 2023-07-13 07:52:56 more
  • c語言學習4

    一、陣列 什么是陣列：變數的組合，是一種批量定義相同型別變數的方式 定義： 型別名 陣列名[數量]; int arr[5]; 注意：陣列的長度一旦確定，無法改變 使用：陣列名[下標]; 下標：從0開始，范圍：0~數量-1 遍歷：把陣列的資料從頭到尾顯示或訪問 一般與for回圈配合，把回圈變數i當做數 ......

    uj5u.com 2023-07-13 07:52:52 more
  • Docker學習路線3：安裝設定

    Docker提供了一個名為**Docker Desktop**的桌面應用程式，簡化了安裝和設定程序。還有另一個選項可以使用**Docker引擎**進行安裝。 - [Docker Desktop網站](https://www.docker.com/products/docker-desktop/) - ......

    uj5u.com 2023-07-13 07:51:28 more

Copyright © 2010-2020 有解無憂